Introduction

• ARIMA models

• ETS models

• Dynamic regression models: How to include external variables

Regression model

yt=β0+β1x1,t+...+βkxk,t+ϵt$$y_t={\beta }_0+{\beta }_1{x}_{1,t}+...+{\beta }_k{x}_{k,t}+{ϵ}_t$$

Allow the errors from a regression to contain autocorrelation.

yt=β0+β1x1,t+...+βkxk,t+ηt$$y_t={\beta }_0+{\beta }_1{x}_{1,t}+...+{\beta }_k{x}_{k,t}+{\eta }_t$$ (1−ϕ1B)(1−B)ηt=(1+θ1B)ϵt$$(1-{\varphi }_{1}B)(1-B){\eta }_t=(1+{\theta }_{1}B){ϵ}_t$$

where ϵt${ϵ}_t$ is a white noise series.

ηt${\eta }_t$ follows an ARIMA(1,1,1)$ARIMA(1,1,1)$

Stationary variables vs Nonstationary Variables

• If all of the variables in the model are stationary, then we only need to consider ARMA errors for the residuals

• Regression model with ARIMA errors is equivalent to a regression model in differences with ARMA errors.

y′t=β0+β1x′1,t+...+βkx′k,t+η′t$$y_t^{\prime }={\beta }_0+{\beta }_1{x}_{1,t}^{\prime }+...+{\beta }_k{x}_{k,t}^{\prime }+{\eta }_t^{\prime }$$

(1−ϕ1B)η′t=(1+θ1B)ϵt$$(1-{\varphi }_{1}B){\eta }_t^{\prime }=(1+{\theta }_{1}B){ϵ}_t$$

y′t=yt−yt−1$$y_t^{\prime }=y_t-y_{t-1}$$

x′t,i=xt,i−xt−1,i$$x_{t,i}^{\prime }=x_{t,i}-x_{t-1,i}$$

η′t=ηt−ηt−1$${\eta }_t^{\prime }={\eta }_t-{\eta }_{t-1}$$

Regression with ARIMA errors in R

To fit

y′t=β1x′t+η′t,$$y_t^{\prime }={\beta }_1{x}_t^{\prime }+{\eta }_t^{\prime },$$

where η′t=ϕ1η′t−1+ϵt${\eta }_t^{\prime }={\varphi }_1{\eta }_{t-1}^{\prime }+{ϵ}_t$ is an AR(1)$AR\left(1\right)$ error.

This is equivalent to

yt=β0+β1xt+ηt$$y_t={\beta }_0+{\beta }_1{x}_t+{\eta }_t$$ where ηt${\eta }_t$ is an ARIMA(1,1,0)$ARIMA(1,1,0)$ error.

Constant term disappears due to the differencing.

fit <- Arima(y, xreg=x, order=c(1,1,0))

Using automated ARIMA algorithm

library(forecast)
library(fpp2)
head(uschange)

        Consumption     Income Production   Savings Unemployment
1970 Q1   0.6159862  0.9722610 -2.4527003 4.8103115          0.9
1970 Q2   0.4603757  1.1690847 -0.5515251 7.2879923          0.5
1970 Q3   0.8767914  1.5532705 -0.3587079 7.2890131          0.5
1970 Q4  -0.2742451 -0.2552724 -2.1854549 0.9852296          0.7
1971 Q1   1.8973708  1.9871536  1.9097341 3.6577706         -0.1
1971 Q2   0.9119929  1.4473342  0.9015358 6.0513418         -0.1

Using automated ARIMA algorithm

autoplot(uschange[,1:2], facets=TRUE) +
xlab("Year") + ylab("") +
ggtitle("Quarterly changes in US consumption
and personal income")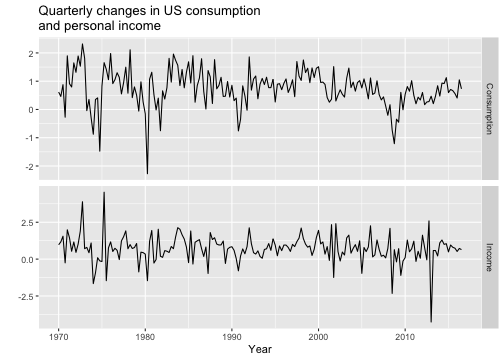

Using automated ARIMA algorithm

fit <- auto.arima(uschange[,"Consumption"],
xreg=uschange[,"Income"])
fit

Series: uschange[, "Consumption"] 
Regression with ARIMA(1,0,2) errors 
Coefficients:
         ar1      ma1     ma2  intercept    xreg
      0.6922  -0.5758  0.1984     0.5990  0.2028
s.e.  0.1159   0.1301  0.0756     0.0884  0.0461
sigma^2 estimated as 0.3219:  log likelihood=-156.95
AIC=325.91   AICc=326.37   BIC=345.29

The fitted model is

ˆyt=0.599+0.203xt+ηt${\hat{y}}_t=0.599+0.203x_t+{\eta }_t$

ηt=0.692ηt−1+ϵt−0.576ϵt−1+0.198ϵt−2${\eta }_t=0.692{\eta }_{t-1}+{ϵ}_t-0.576{ϵ}_{t-1}+0.198{ϵ}_{t-2}$

ϵt∼NID(0,0.322)${ϵ}_t\sim NID(0,0.322)$

plot ηt${\eta }_t$ and ϵt${ϵ}_t$

residuals function can be used to extract ηt${\eta }_t$ and ϵt${ϵ}_t$.

library(magrittr)
cbind("Regression Errors" = residuals(fit, type="regression"),
"ARIMA errors" = residuals(fit, type="innovation")) %>%
autoplot(facets=TRUE)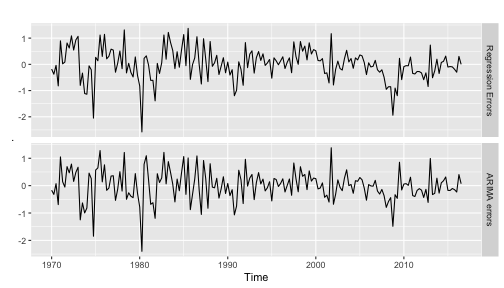

It is the ARIMA errors that should resemble a white noise series.

checkresiduals(fit)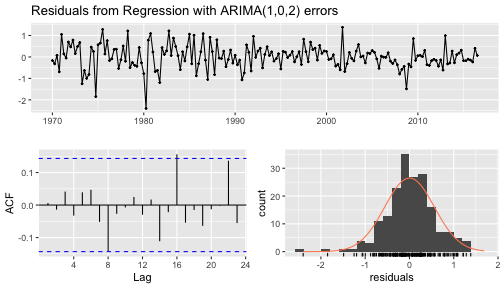

    Ljung-Box test
data:  Residuals from Regression with ARIMA(1,0,2) errors
Q* = 5.8916, df = 3, p-value = 0.117
Model df: 5.   Total lags used: 8

Calculate forecasts

1. We first need to forecast predictors

fcast <- forecast(fit, xreg=rep(mean(uschange[,2]),8))
autoplot(fcast) + xlab("Year") + ylab("Percentage change")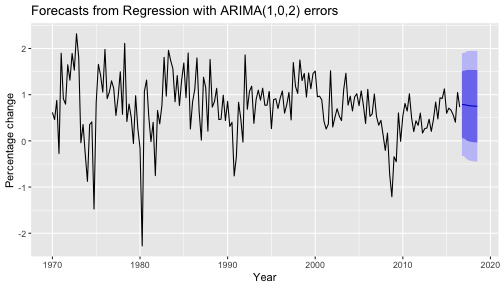

Forecasting electricity demand

Model daily electricity demand as a function of temperature using quadratic regression with ARMA errors.

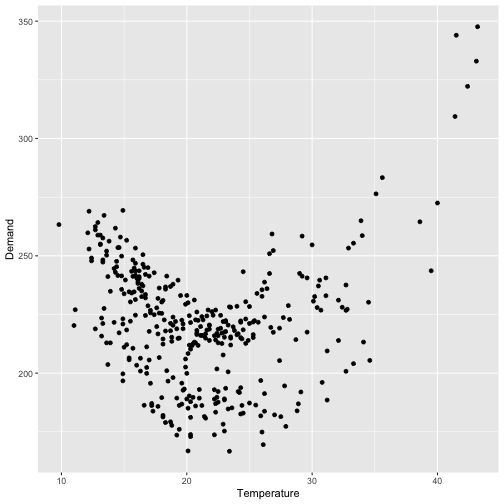
Forecasting electricity demand

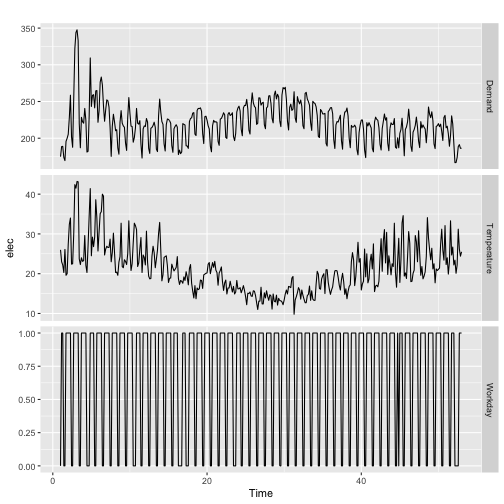
Forecasting electricity demand

xreg <- cbind(MaxTemp = elecdaily[, "Temperature"],
MaxTempSq = elecdaily[, "Temperature"]^2,
Workday = elecdaily[, "WorkDay"])
fit <- auto.arima(elecdaily[, "Demand"], xreg = xreg)
fit

Series: elecdaily[, "Demand"] 
Regression with ARIMA(2,1,2)(2,0,0)[7] errors 
Coefficients:
          ar1     ar2      ma1      ma2    sar1    sar2    drift  MaxTemp
      -0.0622  0.6731  -0.0234  -0.9301  0.2012  0.4021  -0.0191  -7.4996
s.e.   0.0714  0.0667   0.0413   0.0390  0.0533  0.0567   0.1091   0.4409
      MaxTempSq  Workday
         0.1789  30.5695
s.e.     0.0084   1.2891
sigma^2 estimated as 43.72:  log likelihood=-1200.7
AIC=2423.4   AICc=2424.15   BIC=2466.27

Forecasting

forecast(fit, xreg = cbind(20, 20^2, 1)) # Forecast one day ahead

         Point Forecast    Lo 80    Hi 80    Lo 95    Hi 95
53.14286       185.4008 176.9271 193.8745 172.4414 198.3602

Forecasting electricity demand (cont.)

checkresiduals(fit)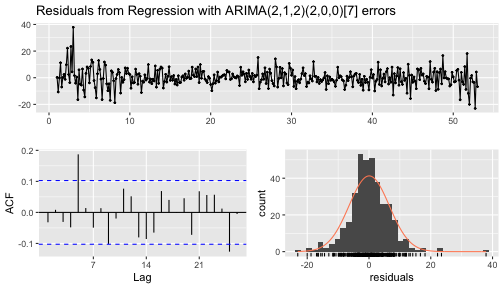

    Ljung-Box test
data:  Residuals from Regression with ARIMA(2,1,2)(2,0,0)[7] errors
Q* = 28.229, df = 4, p-value = 1.121e-05
Model df: 10.   Total lags used: 14

Lagged predictors

yt=β0+γ0xt+γ1xt−1+...+γkxt−k+ηt$$y_t={\beta }_0+{\gamma }_0{x}_t+{\gamma }_1{x}_{t-1}+...+{\gamma }_k{x}_{t-k}+{\eta }_t$$

where ηt${\eta }_t$ is an ARIMA$ARIMA$ process.

How to select k$k$ ?

Use AICc along with the values of p$p$ and q$q$ for the ARIMA error.

autoplot(insurance, facets=TRUE) +
xlab("Year") + ylab("") +
ggtitle("Insurance advertising and quotations")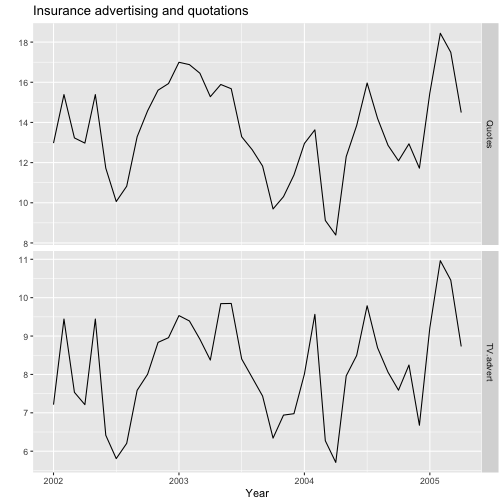

Lagged predictors

Advert <- cbind(
AdLag0 = insurance[,"TV.advert"],
AdLag1 = stats::lag(insurance[,"TV.advert"],-1),
AdLag2 = stats::lag(insurance[,"TV.advert"],-2),
AdLag3 = stats::lag(insurance[,"TV.advert"],-3)) %>%
head(NROW(insurance))
head(Advert)

           AdLag0   AdLag1   AdLag2   AdLag3
Jan 2002 7.212725       NA       NA       NA
Feb 2002 9.443570 7.212725       NA       NA
Mar 2002 7.534250 9.443570 7.212725       NA
Apr 2002 7.212725 7.534250 9.443570 7.212725
May 2002 9.443570 7.212725 7.534250 9.443570
Jun 2002 6.415215 9.443570 7.212725 7.534250

Lagged predictors (cont.)

fit1 <- auto.arima(insurance[4:40,1], xreg=Advert[4:40,1],
stationary=TRUE)
fit1[["aicc"]]

[1] 68.49968

fit2 <- auto.arima(insurance[4:40,1], xreg=Advert[4:40,1:2],
stationary=TRUE)
fit2[["aicc"]]

[1] 60.02357

fit3 <- auto.arima(insurance[4:40,1], xreg=Advert[4:40,1:3],
stationary=TRUE)
fit3[["aicc"]]

[1] 62.83253

fit4 <- auto.arima(insurance[4:40,1], xreg=Advert[4:40,1:4],
stationary=TRUE)
fit4[["aicc"]]

[1] 65.45747

Lagged predictors (cont.)

Re-estimate the model

fit <- auto.arima(insurance[,1], xreg=Advert[,1:2],
stationary=TRUE); fit

Series: insurance[, 1] 
Regression with ARIMA(3,0,0) errors 
Coefficients:
         ar1      ar2     ar3  intercept  AdLag0  AdLag1
      1.4117  -0.9317  0.3591     2.0393  1.2564  0.1625
s.e.  0.1698   0.2545  0.1592     0.9931  0.0667  0.0591
sigma^2 estimated as 0.2165:  log likelihood=-23.89
AIC=61.78   AICc=65.4   BIC=73.43

The fitted model is

yt=2.039+1.25xt+0.162xt−1+ηt$$y_t=2.039+1.25x_t+0.162x_{t-1}+{\eta }_t$$ ηt=1.412ηt−1−0.932ηt−2+0.359ηt−3+ϵt$${\eta }_t=1.412{\eta }_{t-1}-0.932{\eta }_{t-2}+0.359{\eta }_{t-3}+{ϵ}_t$$

yt$y_t$ - the number of quotations provided in month t$t$

xt$x_t$ - the advertising expenditure in month t$t$

ϵt${ϵ}_t$ is white noise.

Generate forecasts

fc8 <- forecast(fit, h=20,
xreg=cbind(AdLag0 = rep(8,20),
AdLag1 = c(Advert[40,1], rep(8,19))))
autoplot(fc8) + ylab("Quotes") +
ggtitle("Forecast quotes with future advertising set to 8")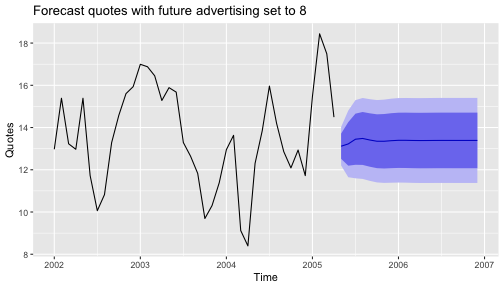

checkresiduals(fc8)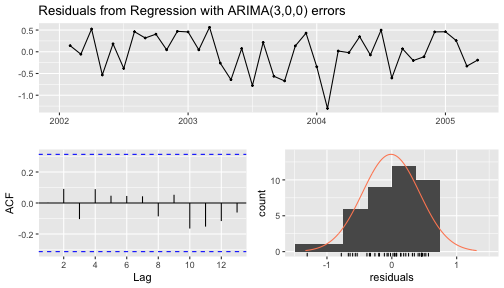

    Ljung-Box test
data:  Residuals from Regression with ARIMA(3,0,0) errors
Q* = 2.0324, df = 3, p-value = 0.5657
Model df: 6.   Total lags used: 9

Other approaches

• Neural network models

• Machine learning approaches

• TBATS models

• Forecasting with decomposition

• Vector autoregressions