IM532 3.0 Applied Time Series ForecastingExponential Smoothing MethodDr Thiyanga Talagala31 May 20201 / 48

Time series decomposition

Recall: Time series patterns

Trend ( $T_{t}$ )

Long-term increase or decrease in the data.

Seasonal ( $S_{t}$ )

A seasonal pattern exists when a series is influenced by seasonal factors (e.g., the quarter of the year, the month, or day of the week). Seasonality is always of a fixed and known period. Hence, seasonal time series are sometimes called periodic time series.

Period is unchanging and associated with some aspect of the calendar.

Cyclic

A cyclic pattern exists when data exhibit rises and falls that are not of fixed period. The duration of these fluctuations is usually of at least 2 years.

2 / 48

Time series decomposition

$y_{t} = f (S_{t}, T_{t}, R_{t})$

$y_{t}$ : data at period $t$ .

$T_{t}$ : trend-cycle component at period $t$ .

$S_{t}$ : seasonal component at period $t$ .

$R_{t}$ : remainder component at period $t$ .

Additive decomposition

$y_{t} = S_{t} + T_{t} + R_{t}$

Multiplicative decomposition

$y_{t} = S_{t} \times T_{t} \times R_{t}$

To transform from multiplicative to additive, you can use a Box-Cox transformation (particularly, log transformation).

3 / 48

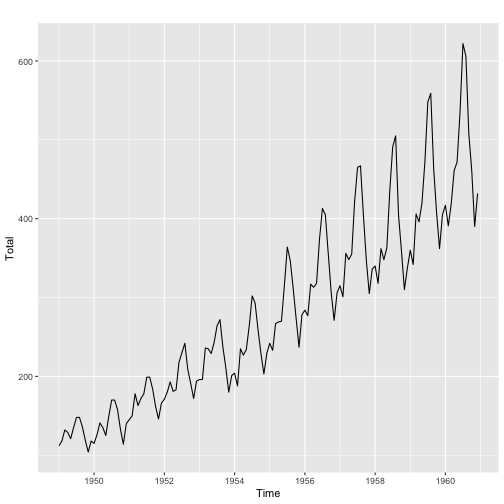
Multiplicative vs. Additive

Multiplicative

AirPassengers

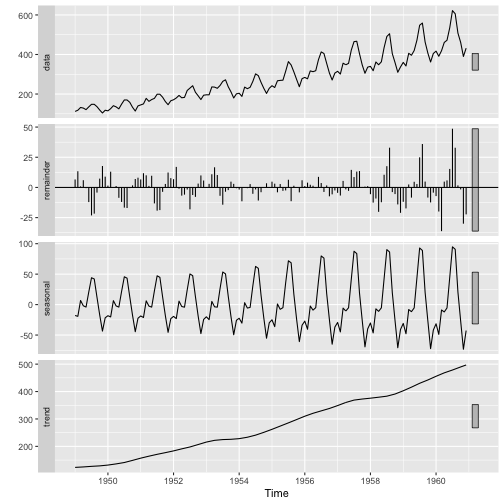
Additive

log(AirPassengers)

4 / 48

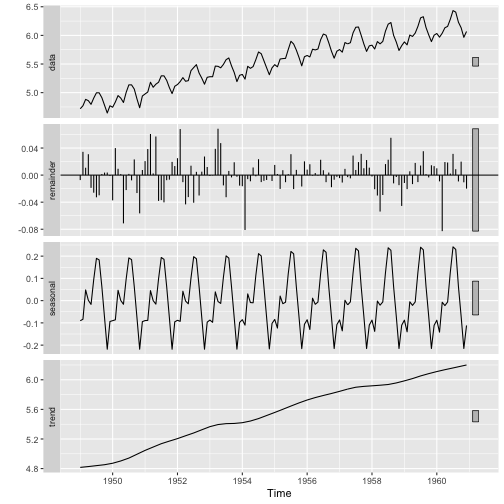
ExponenTial Smoothing Models (ETS models)5 / 48

6 / 48

Introduction

Naive approach

${\hat{Y}}_{t + h | t} = y_{t}$

Average method

${\hat{Y}}_{t + h | t} = \bar{y} = (y_{1} + y_{2} + . . . + y_{t}) / t$

Exponential smoothing method

${\hat{Y}}_{t + 1 | t} = α y_{t} + (1 - α) {\hat{Y}}_{t}$

where $0 < α < 1$ .

$New forecast = [α \times New observed value] + [(1 - α) \times Previous forecast]$ $α$ - smoothing constant

7 / 48

Exponential Smoothing Method

8 / 48

Exponential Smoothing Method

$\begin{array}{rcl} {\hat{Y}}_{t + 1 | t} & = & α y_{t} + (1 - α) {\hat{Y}}_{t} \\ = & α y_{t} + (1 - α) [α y_{t - 1} + (1 - α) {\hat{Y}}_{t - 1}] \\ = & α y_{t} + α (1 - α) y_{t - 1} + (1 - α)^{2} {\hat{Y}}_{t - 1} \end{array}$ Continued substitution for ${\hat{Y}}_{t - 1}$ and so forth shows ${\hat{Y}}_{t + 1}$ can be written as a sum of current and previous $y$ 's with exponentially declining weights.

${\hat{Y}}_{t + 1 | t} = α y_{t} + α (1 - α) y_{t - 1} + α (1 - α)^{2} y_{t - 2} + α (1 - α)^{3} y_{t - 3} + . . .$ ${\hat{Y}}_{t + 1}$ is an exponentially smoothed value.

8 / 48

Exponential Smoothing Method

${\hat{Y}}_{t + 1 | t} = α y_{t} + α (1 - α) y_{t - 1} + α (1 - α)^{2} y_{t - 2} + α (1 - α)^{3} y_{t - 3} + . . .$ ${\hat{Y}}_{t + 1}$ is an exponentially smoothed value.

The speed at which past observations lose their impact depends on the value of $α$ .

8 / 48

Exponential Smoothing Method

${\hat{Y}}_{t + 1 | t} = α y_{t} + α (1 - α) y_{t - 1} + α (1 - α)^{2} y_{t - 2} + α (1 - α)^{3} y_{t - 3} + . . .$ ${\hat{Y}}_{t + 1}$ is an exponentially smoothed value.

The speed at which past observations lose their impact depends on the value of $α$ .

The $α$ producing the smallest forecast error is chosen for use in calculating future forecasts.

8 / 48

Comparison of different values for αα

Period
α=0.1α=0.1
α=0.6α=0.6 


tt
.100.100
.600.600

t−1t−1
.9×.1=.090.9×.1=.090
.4×.6=.240.4×.6=.240

t−2t−2
.9×.9×.1=.081.9×.9×.1=.081
.4×.4×.6=.096.4×.4×.6=.096

t−3t−3
.9×.9×.9×.1=.073.9×.9×.9×.1=.073
.4×.4×.4×.6=.038.4×.4×.4×.6=.038

t−4t−4
.9×.9×.9×.9×.1=.066.9×.9×.9×.9×.1=.066
.4×.4×.4×.4×.6=.015.4×.4×.4×.4×.6=.015

..
..
..

..
..
..

..
..
..

9 / 48

Comparison of different values for $α$

Period	$α = 0.1$	$α = 0.6$
$t$	$.100$	$.600$
$t - 1$	$.9 \times .1 = .090$	$.4 \times .6 = .240$
$t - 2$	$.9 \times .9 \times .1 = .081$	$.4 \times .4 \times .6 = .096$
$t - 3$	$.9 \times .9 \times .9 \times .1 = .073$	$.4 \times .4 \times .4 \times .6 = .038$
$t - 4$	$.9 \times .9 \times .9 \times .9 \times .1 = .066$	$.4 \times .4 \times .4 \times .4 \times .6 = .015$
$.$	$.$	$.$
$.$	$.$	$.$
$.$	$.$	$.$

Factors that affects the values of forecasts

${\hat{Y}}_{t + 1 | t} = α y_{t} + α (1 - α) y_{t - 1} + α (1 - α)^{2} y_{t - 2} + α (1 - α)^{3} y_{t - 3} + . . .$

choice of $α$
initial value $y_{t}$

9 / 48

Single Exponential Smoothing (SES)

Suitable when data has no clear trend or seasonal pattern.

Component form

Forecasting equation

${\hat{Y}}_{t + h | t} = l_{t}$

Smoothing equation

$l_{t} = α y_{t} + (1 - α) l_{t - 1}$

$l_{t}$ - level (or smoothed value) at time $t$

Weighted average form

${\hat{Y}}_{t + 1 | t} = \sum_{j = 0}^{t - 1} α (1 - α)^{j} y_{t - j} + (1 - α)^{t} l_{0}$

10 / 48

How to find $α$ and $l_{0}$ ?

minimizing SSE

$S S E = \sum_{t = 1}^{T} (y_{t} - {\hat{Y}}_{t | t - 1})^{2} = \sum_{t = 1}^{T} e_{t}^{2}$

11 / 48

Example

Calculate forecasts for 2020 and 2021.

$y_{2019} = 92.04$ $y_{2020} = 81.44$

${\hat{Y}}_{2019} = 86.46$

Find ${\hat{Y}}_{2020}$ and ${\hat{Y}}_{2021}$ when $α = 0.04$ .

12 / 48

Example: oil production

# forecast, fpp2
autoplot(oil)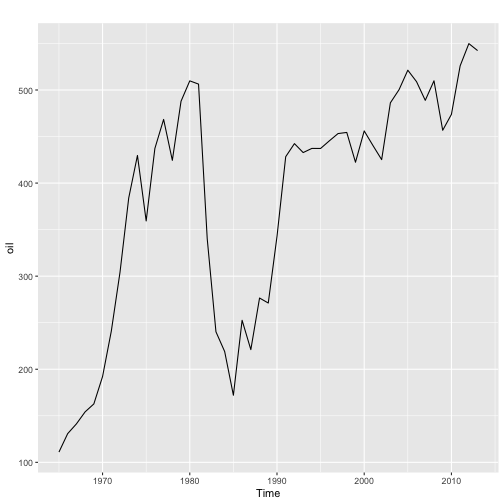

13 / 48

Example: oil production (cont.)

oil1996 <- window(oil, start = 1996)
ses.fcast <- ses(oil1996, h=5)
ses.fcast

     Point Forecast    Lo 80    Hi 80    Lo 95    Hi 95
2014       542.6806 504.4541 580.9070 484.2183 601.1429
2015       542.6806 492.9073 592.4539 466.5589 618.8023
2016       542.6806 483.5747 601.7864 452.2860 633.0752
2017       542.6806 475.5269 609.8343 439.9778 645.3834
2018       542.6806 468.3452 617.0159 428.9945 656.3667

14 / 48

Example: oil production (cont.)

summary(ses.fcast)


Forecast method: Simple exponential smoothing
Model Information:
Simple exponential smoothing 
Call:
 ses(y = oil1996, h = 5) 
  Smoothing parameters:
    alpha = 0.8339 
  Initial states:
    l = 446.5868 
  sigma:  29.8282
     AIC     AICc      BIC 
178.1430 179.8573 180.8141 
Error measures:
                   ME     RMSE     MAE      MPE     MAPE      MASE        ACF1
Training set 6.401975 28.12234 22.2587 1.097574 4.610635 0.9256774 -0.03377748
Forecasts:
     Point Forecast    Lo 80    Hi 80    Lo 95    Hi 95
2014       542.6806 504.4541 580.9070 484.2183 601.1429
2015       542.6806 492.9073 592.4539 466.5589 618.8023
2016       542.6806 483.5747 601.7864 452.2860 633.0752
2017       542.6806 475.5269 609.8343 439.9778 645.3834
2018       542.6806 468.3452 617.0159 428.9945 656.3667

15 / 48

Example: oil production (cont.)

ses.fcast %>%
  autoplot() +
  ylab("Oil production (millions of tonnes)") + xlab("Year")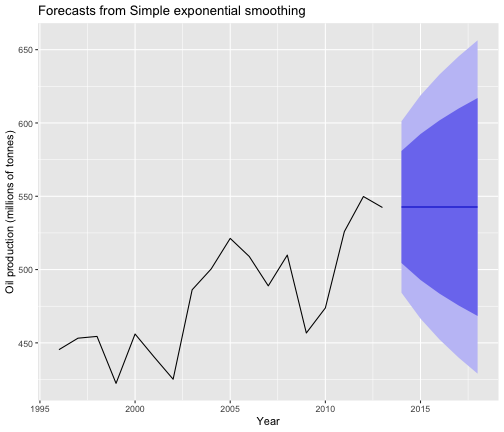

16 / 48

Exponential Smoothing ModelsTrend Methods17 / 48

Holt's linear trend

Component form

Forecasting equation

${\hat{Y}}_{t + h | t} = l_{t} + h b_{t}$

Smoothing equation

$l_{t} = α y_{t} + (1 - α) (l_{t - 1} - b_{t - 1})$ Trend

$b_{t} = β^{*} (l_{t} - l_{t - 1}) + (1 - β^{*}) b_{t - 1}$

Smoothing parameters

$0 \leq α \leq 1$ $0 \leq β^{*} \leq 1$ Choose $α$ , $β^{*}$ , $l_{0}$ and $b_{0}$ minimizing SSE.

18 / 48

Example: Sri Lanka GDP

slgdp <- c(56.73, 65.29, 68.43, 74.32, 79.36, 80.6, 82.4, 88.02, 88.9, 91)
slgdp.ts <- ts(slgdp, start=2010)
autoplot(slgdp.ts)+ggtitle("Sri Lanka GDP")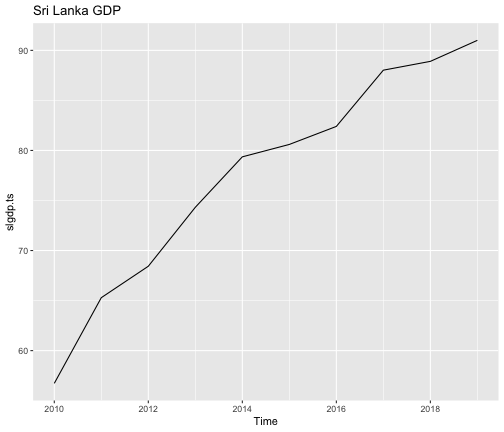

19 / 48

Example: Sri Lanka GDP (cont)

fcast.holt <- slgdp.ts %>% holt(h=5)
fcast.holt

     Point Forecast     Lo 80    Hi 80     Lo 95    Hi 95
2020       96.99317  93.18154 100.8048  91.16378 102.8226
2021      100.52190  96.71027 104.3335  94.69251 106.3513
2022      104.05064 100.23900 107.8623  98.22124 109.8800
2023      107.57937 103.76773 111.3910 101.74997 113.4088
2024      111.10810 107.29646 114.9197 105.27871 116.9375

fcast.holt %>% autoplot()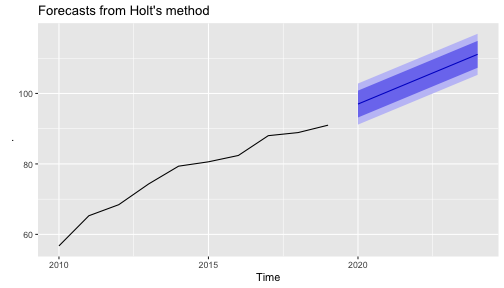

20 / 48

Example: Sri Lanka GDP (cont)

summary(fcast.holt)


Forecast method: Holt's method
Model Information:
Holt's method 
Call:
 holt(y = ., h = 5) 
  Smoothing parameters:
    alpha = 1e-04 
    beta  = 1e-04 
  Initial states:
    l = 58.1775 
    b = 3.5288 
  sigma:  2.9742
     AIC     AICc      BIC 
49.71733 64.71733 51.23025 
Error measures:
                      ME     RMSE      MAE        MPE     MAPE      MASE
Training set -0.07963403 2.303832 1.777759 -0.3047917 2.437425 0.4668757
                  ACF1
Training set 0.2014695
Forecasts:
     Point Forecast     Lo 80    Hi 80     Lo 95    Hi 95
2020       96.99317  93.18154 100.8048  91.16378 102.8226
2021      100.52190  96.71027 104.3335  94.69251 106.3513
2022      104.05064 100.23900 107.8623  98.22124 109.8800
2023      107.57937 103.76773 111.3910 101.74997 113.4088
2024      111.10810 107.29646 114.9197 105.27871 116.9375

21 / 48

Damped trend method

Component form

Forecasting equation

${\hat{Y}}_{t + h | t} = l_{t} + (ϕ + ϕ^{2} + . . . + ϕ^{h})$

Smoothing equation

$l_{t} = α y_{t} + (1 - α) (l_{t - 1} - ϕ b_{t - 1})$ Trend

$b_{t} = β^{*} (l_{t} - l_{t - 1}) + (1 - β^{*}) ϕ b_{t - 1}$

Damping parameter: $0 < ϕ < 1$ .

If $ϕ = 1$ , identical to Holt's linear trend.

22 / 48

Example

fcast_holt <- slgdp.ts %>% holt(h=7)
fcast_holt_damped <- slgdp.ts %>% holt(h=7, damped = TRUE)
autoplot(slgdp.ts) + xlab("Year") + ylab("GDP")+
  autolayer(fcast.holt, series="Linear trend")+
  autolayer(fcast_holt_damped, series="Damped trend")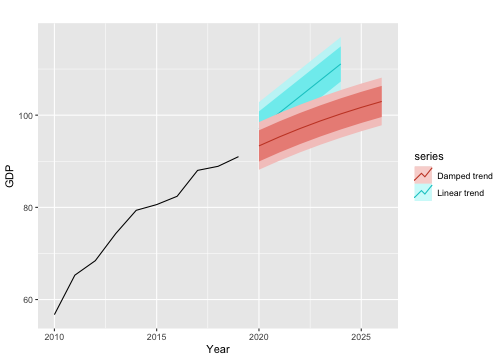

23 / 48

Exponential Smoothing ModelsTrend + Seasonal24 / 48

Holt-Winters' additive method

Component form

Forecasting equation

${\hat{Y}}_{t + h | t} = l_{t} + h b_{t} + s_{t - m + h_{m}^{+}}$

Smoothing equation

$l_{t} = α (y_{t} - s_{t - m}) + (1 - α) (l_{t - 1} + b_{t - 1})$ $b_{t} = β^{*} (l_{t} - l_{t - 1}) + (1 - β^{*}) b_{t - 1}$ $s_{t} = γ (y_{t} - l_{t - 1} - b_{t - 1}) + (1 - γ) s_{t - m}$

$s_{t - 1 + h_{m}^{+}}$ - seasonal component from last year of data
Smoothing parameters:

$0 \leq α \leq 1$ , $0 \leq β^{*} \leq 1$ and $0 \leq γ \leq 1 - α$

m: seasonal period

25 / 48

Holt-Winters' multiplicative method

Component form

Forecasting equation

${\hat{Y}}_{t + h | t} = (l_{t} + h b_{t}) s_{t - m + h_{m}^{+}}$

Smoothing equation

$l_{t} = α \frac{y_{t}}{s_{t - m}} + (1 - α) (l_{t - 1} + b_{t - 1})$ $b_{t} = β^{*} (l_{t} - l_{t - 1}) + (1 - β^{*}) b_{t - 1}$ $s_{t} = γ \frac{y_{t}}{(l_{t - 1} + b_{t - 1})} + (1 - γ) s_{t - m}$

$s_{t - 1 + h_{m}^{+}}$ - seasonal component from last year of data
Smoothing parameters:

$0 \leq α \leq 1$ , $0 \leq β^{*} \leq 1$ and $0 \leq γ \leq 1 - α$

m: seasonal period

26 / 48

Example

AirPassengers.trn <- window(AirPassengers, end=c(1959, 12))
fcast.additive <- hw(AirPassengers.trn, seasonal="additive", h=12)
fcast.multiplicative <- hw(AirPassengers.trn, seasonal="multiplicative", 
                           h=12)

fcast.additive

         Point Forecast    Lo 80    Hi 80    Lo 95    Hi 95
Jan 1960       409.2577 388.1899 430.3256 377.0373 441.4782
Feb 1960       402.8045 373.0119 432.5970 357.2407 448.3683
Mar 1960       439.0902 402.5995 475.5810 383.2824 494.8980
Apr 1960       430.7499 388.6097 472.8900 366.3021 495.1977
May 1960       433.3781 386.2587 480.4976 361.3151 505.4411
Jun 1960       474.8847 423.2618 526.5077 395.9342 553.8353
Jul 1960       502.6950 446.9289 558.4611 417.4082 587.9819
Aug 1960       504.2110 444.5870 563.8349 413.0240 595.3980
Sep 1960       461.0817 397.8328 524.3305 364.3509 557.8124
Oct 1960       426.6746 359.9959 493.3533 324.6983 528.6509
Nov 1960       398.6437 328.7014 468.5860 291.6762 505.6112
Dec 1960       424.4781 351.4162 497.5399 312.7396 536.2165

27 / 48

Example (cont.)

fcast.multiplicative

         Point Forecast    Lo 80    Hi 80    Lo 95    Hi 95
Jan 1960       416.6188 394.3272 438.9105 382.5267 450.7110
Feb 1960       393.6628 371.3633 415.9624 359.5587 427.7670
Mar 1960       462.3467 434.7187 489.9747 420.0934 504.6001
Apr 1960       448.5228 420.3370 476.7085 405.4164 491.6291
May 1960       472.2089 441.0871 503.3307 424.6123 519.8055
Jun 1960       540.0026 502.7660 577.2392 483.0542 596.9510
Jul 1960       625.6443 580.6024 670.6862 556.7586 694.5300
Aug 1960       635.3948 587.7281 683.0615 562.4948 708.2947
Sep 1960       520.6261 479.9980 561.2542 458.4908 582.7614
Oct 1960       455.1924 418.2998 492.0850 398.7701 511.6147
Nov 1960       399.6811 366.0861 433.2762 348.3020 451.0603
Dec 1960       440.2986 401.9675 478.6297 381.6763 498.9209

28 / 48

Example (cont.)

summary(fcast.additive)


Forecast method: Holt-Winters' additive method
Model Information:
Holt-Winters' additive method 
Call:
 hw(y = AirPassengers.trn, h = 12, seasonal = "additive") 
  Smoothing parameters:
    alpha = 0.9996 
    beta  = 3e-04 
    gamma = 3e-04 
  Initial states:
    l = 121.2277 
    b = 1.597 
    s = -26.7836 -50.9792 -21.3319 14.7009 59.4508 59.53
           33.3833 -6.519 -7.5225 2.4467 -32.2225 -24.153
  sigma:  16.4393
     AIC     AICc      BIC 
1400.588 1405.957 1449.596 
Error measures:
                    ME     RMSE      MAE       MPE     MAPE      MASE      ACF1
Training set 0.7468154 15.41083 11.57204 0.2589801 5.002286 0.3800341 0.1636311
Forecasts:
         Point Forecast    Lo 80    Hi 80    Lo 95    Hi 95
Jan 1960       409.2577 388.1899 430.3256 377.0373 441.4782
Feb 1960       402.8045 373.0119 432.5970 357.2407 448.3683
Mar 1960       439.0902 402.5995 475.5810 383.2824 494.8980
Apr 1960       430.7499 388.6097 472.8900 366.3021 495.1977
May 1960       433.3781 386.2587 480.4976 361.3151 505.4411
Jun 1960       474.8847 423.2618 526.5077 395.9342 553.8353
Jul 1960       502.6950 446.9289 558.4611 417.4082 587.9819
Aug 1960       504.2110 444.5870 563.8349 413.0240 595.3980
Sep 1960       461.0817 397.8328 524.3305 364.3509 557.8124
Oct 1960       426.6746 359.9959 493.3533 324.6983 528.6509
Nov 1960       398.6437 328.7014 468.5860 291.6762 505.6112
Dec 1960       424.4781 351.4162 497.5399 312.7396 536.2165

summary(fcast.multiplicative)


Forecast method: Holt-Winters' multiplicative method
Model Information:
Holt-Winters' multiplicative method 
Call:
 hw(y = AirPassengers.trn, h = 12, seasonal = "multiplicative") 
  Smoothing parameters:
    alpha = 0.3392 
    beta  = 0.0105 
    gamma = 0.6534 
  Initial states:
    l = 122.569 
    b = 1.51 
    s = 0.9296 0.7992 0.9096 1.0615 1.1326 1.177
           1.0374 0.9334 1.0075 1.0984 0.9852 0.9288
  sigma:  0.0418
     AIC     AICc      BIC 
1270.460 1275.829 1319.468 
Error measures:
                   ME     RMSE      MAE       MPE    MAPE      MASE      ACF1
Training set 1.369382 9.949946 7.533284 0.2993092 2.99775 0.2473985 0.3047973
Forecasts:
         Point Forecast    Lo 80    Hi 80    Lo 95    Hi 95
Jan 1960       416.6188 394.3272 438.9105 382.5267 450.7110
Feb 1960       393.6628 371.3633 415.9624 359.5587 427.7670
Mar 1960       462.3467 434.7187 489.9747 420.0934 504.6001
Apr 1960       448.5228 420.3370 476.7085 405.4164 491.6291
May 1960       472.2089 441.0871 503.3307 424.6123 519.8055
Jun 1960       540.0026 502.7660 577.2392 483.0542 596.9510
Jul 1960       625.6443 580.6024 670.6862 556.7586 694.5300
Aug 1960       635.3948 587.7281 683.0615 562.4948 708.2947
Sep 1960       520.6261 479.9980 561.2542 458.4908 582.7614
Oct 1960       455.1924 418.2998 492.0850 398.7701 511.6147
Nov 1960       399.6811 366.0861 433.2762 348.3020 451.0603
Dec 1960       440.2986 401.9675 478.6297 381.6763 498.9209

29 / 48

Example (cont.)

summary(fcast.multiplicative)


Forecast method: Holt-Winters' multiplicative method
Model Information:
Holt-Winters' multiplicative method 
Call:
 hw(y = AirPassengers.trn, h = 12, seasonal = "multiplicative") 
  Smoothing parameters:
    alpha = 0.3392 
    beta  = 0.0105 
    gamma = 0.6534 
  Initial states:
    l = 122.569 
    b = 1.51 
    s = 0.9296 0.7992 0.9096 1.0615 1.1326 1.177
           1.0374 0.9334 1.0075 1.0984 0.9852 0.9288
  sigma:  0.0418
     AIC     AICc      BIC 
1270.460 1275.829 1319.468 
Error measures:
                   ME     RMSE      MAE       MPE    MAPE      MASE      ACF1
Training set 1.369382 9.949946 7.533284 0.2993092 2.99775 0.2473985 0.3047973
Forecasts:
         Point Forecast    Lo 80    Hi 80    Lo 95    Hi 95
Jan 1960       416.6188 394.3272 438.9105 382.5267 450.7110
Feb 1960       393.6628 371.3633 415.9624 359.5587 427.7670
Mar 1960       462.3467 434.7187 489.9747 420.0934 504.6001
Apr 1960       448.5228 420.3370 476.7085 405.4164 491.6291
May 1960       472.2089 441.0871 503.3307 424.6123 519.8055
Jun 1960       540.0026 502.7660 577.2392 483.0542 596.9510
Jul 1960       625.6443 580.6024 670.6862 556.7586 694.5300
Aug 1960       635.3948 587.7281 683.0615 562.4948 708.2947
Sep 1960       520.6261 479.9980 561.2542 458.4908 582.7614
Oct 1960       455.1924 418.2998 492.0850 398.7701 511.6147
Nov 1960       399.6811 366.0861 433.2762 348.3020 451.0603
Dec 1960       440.2986 401.9675 478.6297 381.6763 498.9209

30 / 48

Example (cont.)

AirPassengers.test <- window(AirPassengers, start=1960)
accuracy(fcast.additive, AirPassengers.test)

                     ME     RMSE      MAE       MPE     MAPE      MASE
Training set  0.7468154 15.41083 11.57204 0.2589801 5.002286 0.3800341
Test set     33.8375637 53.79669 40.59396 6.0173405 7.689038 1.3331351
                  ACF1 Theil's U
Training set 0.1636311        NA
Test set     0.6670272  0.943033

accuracy(fcast.multiplicative, AirPassengers.test)

                    ME      RMSE       MAE        MPE     MAPE      MASE
Training set  1.369382  9.949946  7.533284  0.2993092 2.997750 0.2473985
Test set     -8.016665 16.583116 11.127665 -1.6894318 2.365723 0.3654406
                   ACF1 Theil's U
Training set  0.3047973        NA
Test set     -0.2976567 0.3561253

31 / 48

Example (cont.)

32 / 48

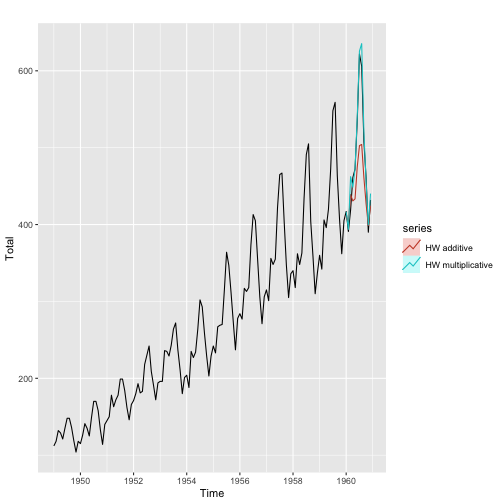
Taxonomy of ETS methods33 / 48

Taxonomy of ETS methods

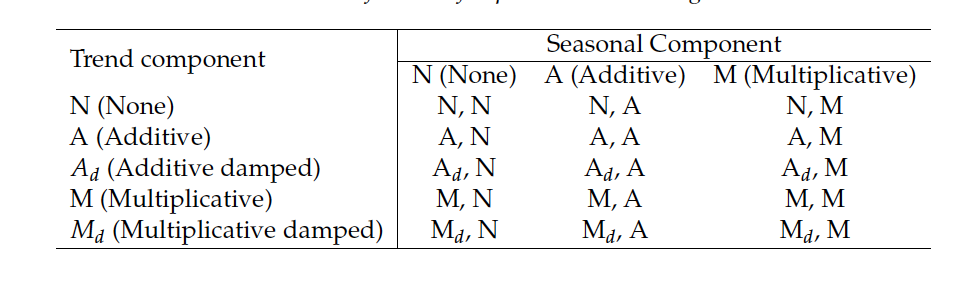
Trend

$(N, N)$ : Simple exponential smoothing - ses()

$(A, N)$ : Holt's linear method - holt()

$(A_{d}, N)$ : Additive damped trend method - hw()

Trend+Seasonal

$(A, A)$ : Additive Holt-Winter's method - hw()

$(A, M)$ : Multiplicative Holt-Winter's method - hw()

$(A_{d}, M)$ : Damped Multiplicative Holt-Winter's method - hw()

34 / 48

Innovations state space models

[Error, Trend, Seasonal]
- Error: $A d d i t i v e - A, M u l t i p l i c a t i v e - M$
- Trend: $N o t r e n d - N, T r e n d - A, D a m p e d t r e n d - A_{d}$
- Seasonal: $N o s e a s o n a l - N, A d d i t i v e - A, M u l t i p l i c a t i v e_{M}$
Example:

$E T S (A, A, A)$

35 / 48

Automated ETS algorithm

30 models $\to$ 19 numerically stable $\to$ 15 models (multiplicative trend gives poor forecast)

The steps involved are summarised below [Hyndman et al., 2008]:

For each series, apply each of the 15 models that are appropriate for the data.
For each model, optimise the parameters (smoothing parameters and initial values for the states) using maximum likelihood estimation.
- For models with additive errors, this is equivalent to minimizing SSE.
Select the best model using the corrected Akaike's Information Criterion (AICc) and produce forecasts using the best selected model.

36 / 48

Automated ETS algorithm in R37 / 48

Automated ETS algorithm in R

ets.auto <- ets(AirPassengers.trn)
ets.auto

ETS(M,Ad,M) 
Call:
 ets(y = AirPassengers.trn) 
  Smoothing parameters:
    alpha = 0.758 
    beta  = 0.0213 
    gamma = 1e-04 
    phi   = 0.98 
  Initial states:
    l = 120.7483 
    b = 1.7632 
    s = 0.897 0.798 0.919 1.0587 1.2156 1.2251
           1.1075 0.9782 0.9804 1.0207 0.8926 0.9073
  sigma:  0.0378
     AIC     AICc      BIC 
1244.458 1250.511 1296.348

38 / 48

Automated ETS algorithm in R (cont.)

auto.ets.fcast <- forecast(ets.auto, h=12)
auto.ets.fcast

         Point Forecast    Lo 80    Hi 80    Lo 95    Hi 95
Jan 1960       411.9115 391.9778 431.8452 381.4255 442.3974
Feb 1960       406.9694 382.0344 431.9043 368.8346 445.1041
Mar 1960       467.3486 433.5448 501.1524 415.6501 519.0470
Apr 1960       450.7386 413.6375 487.8397 393.9974 507.4798
May 1960       451.5327 410.1879 492.8776 388.3012 514.7642
Jun 1960       513.2314 461.7576 564.7052 434.5091 591.9538
Jul 1960       569.8868 507.9846 631.7890 475.2156 664.5580
Aug 1960       567.5873 501.3865 633.7882 466.3419 668.8328
Sep 1960       496.1471 434.4291 557.8652 401.7575 590.5368
Oct 1960       432.2153 375.1873 489.2432 344.9985 519.4320
Nov 1960       376.6263 324.1565 429.0961 296.3807 456.8719
Dec 1960       424.7869 362.5403 487.0334 329.5889 519.9848

39 / 48

Automated ETS algorithm in R (cont.)

auto.ets.fcast %>% autoplot()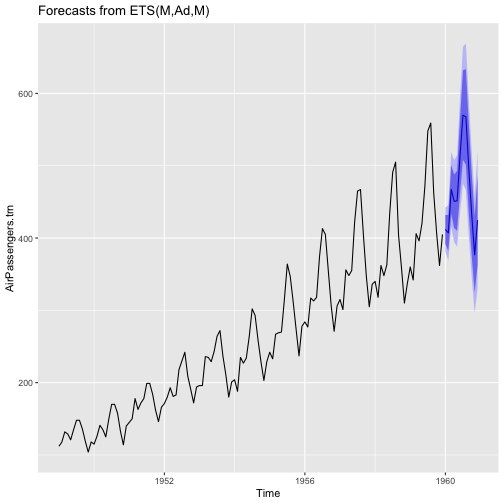

40 / 48

Automated ETS algorithm in R (cont.)

accuracy(auto.ets.fcast, AirPassengers.test)

##                     ME      RMSE       MAE       MPE     MAPE      MASE
## Training set  1.511141  9.353686  6.980909 0.4422335 2.761156 0.2292581
## Test set     12.084843 27.398040 22.804502 2.0517668 4.655647 0.7489163
##                   ACF1 Theil's U
## Training set 0.0457192        NA
## Test set     0.4844065 0.5419859

41 / 48

Comparison

accuracy(auto.ets.fcast, AirPassengers.test)

                    ME      RMSE       MAE       MPE     MAPE      MASE
Training set  1.511141  9.353686  6.980909 0.4422335 2.761156 0.2292581
Test set     12.084843 27.398040 22.804502 2.0517668 4.655647 0.7489163
                  ACF1 Theil's U
Training set 0.0457192        NA
Test set     0.4844065 0.5419859

Previous results: Holt-Winters' additive method and Holt-Winters' multiplicative method

accuracy(fcast.additive, AirPassengers.test)

                     ME     RMSE      MAE       MPE     MAPE      MASE
Training set  0.7468154 15.41083 11.57204 0.2589801 5.002286 0.3800341
Test set     33.8375637 53.79669 40.59396 6.0173405 7.689038 1.3331351
                  ACF1 Theil's U
Training set 0.1636311        NA
Test set     0.6670272  0.943033

accuracy(fcast.multiplicative, AirPassengers.test)

                    ME      RMSE       MAE        MPE     MAPE      MASE
Training set  1.369382  9.949946  7.533284  0.2993092 2.997750 0.2473985
Test set     -8.016665 16.583116 11.127665 -1.6894318 2.365723 0.3654406
                   ACF1 Theil's U
Training set  0.3047973        NA
Test set     -0.2976567 0.3561253

42 / 48

Check Residuals

checkresiduals(ets.auto)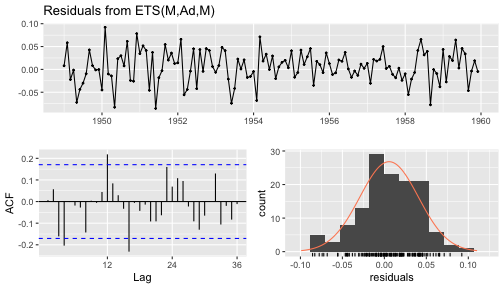


    Ljung-Box test
data:  Residuals from ETS(M,Ad,M)
Q* = 38.252, df = 7, p-value = 2.714e-06
Model df: 17.   Total lags used: 24

43 / 48

Check Residuals (cont.)

checkresiduals(fcast.additive)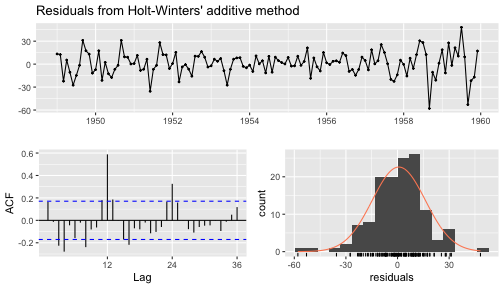


    Ljung-Box test
data:  Residuals from Holt-Winters' additive method
Q* = 135.55, df = 8, p-value < 2.2e-16
Model df: 16.   Total lags used: 24

44 / 48

Check Residuals (cont.)

checkresiduals(fcast.multiplicative)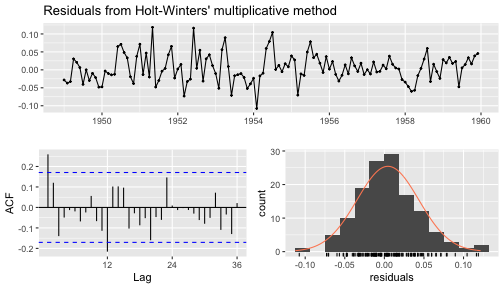


    Ljung-Box test
data:  Residuals from Holt-Winters' multiplicative method
Q* = 41.164, df = 8, p-value = 1.943e-06
Model df: 16.   Total lags used: 24

45 / 48

Your turn

Identify a suitable ETS to forecast Australian air traffic data.

autoplot(ausair)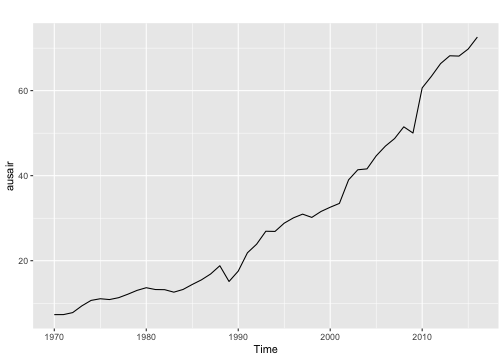

46 / 48

ausair

Time Series:
Start = 1970 
End = 2016 
Frequency = 1 
 [1]  7.31870  7.32660  7.79560  9.38460 10.66470 11.05510 10.86430 11.30650
 [9] 12.12230 13.02250 13.64880 13.21950 13.18790 12.60150 13.23680 14.41210
[17] 15.49730 16.88020 18.81630 15.11430 17.55340 21.86010 23.88660 26.92930
[25] 26.88850 28.83140 30.07510 30.95350 30.18570 31.57970 32.57757 33.47740
[33] 39.02158 41.38643 41.59655 44.65732 46.95177 48.72884 51.48843 50.02697
[41] 60.64091 63.36031 66.35527 68.19795 68.12324 69.77935 72.59770

ausair.tr <- window(ausair, end=2011)
ausair.tr

Time Series:
Start = 1970 
End = 2011 
Frequency = 1 
 [1]  7.31870  7.32660  7.79560  9.38460 10.66470 11.05510 10.86430 11.30650
 [9] 12.12230 13.02250 13.64880 13.21950 13.18790 12.60150 13.23680 14.41210
[17] 15.49730 16.88020 18.81630 15.11430 17.55340 21.86010 23.88660 26.92930
[25] 26.88850 28.83140 30.07510 30.95350 30.18570 31.57970 32.57757 33.47740
[33] 39.02158 41.38643 41.59655 44.65732 46.95177 48.72884 51.48843 50.02697
[41] 60.64091 63.36031

47 / 48

ausair.test <- window(ausair, start=2012)
ausair.test

Time Series:
Start = 2012 
End = 2016 
Frequency = 1 
[1] 66.35527 68.19795 68.12324 69.77935 72.59770

48 / 48

Time series decomposition

Recall: Time series patterns

Trend (

T_{t}

)

Long-term increase or decrease in the data.

Seasonal (

S_{t}

)

Period is unchanging and associated with some aspect of the calendar.

Cyclic

A cyclic pattern exists when data exhibit rises and falls that are not of fixed period. The duration of these fluctuations is usually of at least 2 years.

2 / 48

Help

Keyboard shortcuts

↑, ←, Pg Up, k

Go to previous slide

↓, →, Pg Dn, Space, j

Go to next slide

Home

Go to first slide

End

Go to last slide

Number + Return

Go to specific slide

b / m / f

Toggle blackout / mirrored / fullscreen mode

Clone slideshow

Toggle presenter mode

Start & Stop the presentation timer

Reset the presentation timer

?, h

Toggle this help

IM532 3.0 Applied Time Series Forecasting

Exponential Smoothing Method

Dr Thiyanga Talagala

31 May 2020