IM532 3.0 Applied Time Series ForecastingMSc in Industrial MathematicsIntroduction to ARIMA models8 March 20201 / 38

Stochastic processes

"A statistical phenomenon that evolves in time according to probabilistic laws is called a stochastic process." (Box, George EP, et al. Time series analysis: forecasting and control.)

2 / 38

Stochastic processes

"A statistical phenomenon that evolves in time according to probabilistic laws is called a stochastic process." (Box, George EP, et al. Time series analysis: forecasting and control.)

Non-deterministic time series or statistical time series

A sample realization from an infinite population of time series that could have been generated by a stochastic process.

2 / 38

Stochastic processes

"A statistical phenomenon that evolves in time according to probabilistic laws is called a stochastic process." (Box, George EP, et al. Time series analysis: forecasting and control.)

Non-deterministic time series or statistical time series

A sample realization from an infinite population of time series that could have been generated by a stochastic process.

Probabilistic time series model

Let ${X_{1}, X_{2}, . . .}$ be a sequence of random variables. Then the joint distribution of the random vector $[X_{1}, X_{2}, . . ., X_{n}]^{'}$ is

$P [X_{1} \leq x_{1}, X_{2} \leq x_{2}, . . ., X_{n} \leq x_{n}]$

where $- \infty < x_{1}, . . ., x_{n} < \infty$ and $n = 1, 2, . . .$

2 / 38

Mean function3 / 38

Mean function

The mean function of ${X_{t}}$ is

$μ_{X} (t) = E (X_{t}) .$

3 / 38

Mean function

The mean function of ${X_{t}}$ is

$μ_{X} (t) = E (X_{t}) .$

Covariance function

The covariance function of ${X_{t}}$ is

$γ_{X} (r, s) = C o v (X_{r}, X_{s}) = E [(X_{r} - μ_{X} (r)) (X_{s} - μ_{X} (s))]$

for all integers $r$ and $s$ .

3 / 38

Mean function

The mean function of ${X_{t}}$ is

$μ_{X} (t) = E (X_{t}) .$

Covariance function

The covariance function of ${X_{t}}$ is

$γ_{X} (r, s) = C o v (X_{r}, X_{s}) = E [(X_{r} - μ_{X} (r)) (X_{s} - μ_{X} (s))]$

for all integers $r$ and $s$ .

The covariance function of ${X_{t}}$ at lag $h$ is defined by $γ_{X} (h) := γ_{X} (h, 0) = γ (t + h, t) = C o v (X_{t + h}, X_{t}) .$

3 / 38

Autocovariance function

The auto covariance function of $X_{t}$ at lag $h$ is

$γ_{X} (h) = C o v (X_{t + h}, X_{t}) .$

4 / 38

Autocovariance function

The auto covariance function of $X_{t}$ at lag $h$ is

$γ_{X} (h) = C o v (X_{t + h}, X_{t}) .$

Autocorrelation function

The autocorrelation function of $X_{t}$ at lag $h$ is

$ρ_{X} (h) = \frac{γ_{X} (h)}{γ_{X} (0)} = C o r (X_{t + h}, X_{t}) .$

4 / 38

Weekly stationary

A time series ${X_{t}}$ is called weekly stationary if

$μ_{X} (t)$ is independent of $t$ .
$γ_{X} (t + h, t)$ is independent of $t$ for each $h$ .

In other words the statistical properties of the time series (mean, variance, autocorrelation, etc.) do not depend on the time at which the series is observed, that is no trend or seasonality. However, a time series with cyclic behaviour (but with no trend or seasonality) is stationary.

5 / 38

Weekly stationary

A time series ${X_{t}}$ is called weekly stationary if

$μ_{X} (t)$ is independent of $t$ .
$γ_{X} (t + h, t)$ is independent of $t$ for each $h$ .

Strict stationarity of a time series

A time series ${X_{t}}$ is called weekly stationary if the random vector $[X_{1}, X_{2} . . ., X_{n}]^{'}$ and $[X_{1 + h}, X_{2 + h} . . ., X_{n + h}]^{'}$ have the same joint distribution for all integers $h$ and $n > 0$ .

5 / 38

Simple time series models

1. iid noise

no trend or seasonal component
observations are independent and identically distributed (iid) random variables with zero mean.
Notation: ${X_{t}} \sim I I D (0, σ^{2})$
plays an important role as a building block for more complicated time series.

Joint distribution function of iid noise

$P [X_{1} \leq x_{1}, X_{2} \leq x_{2}, . . ., X_{n} \leq x_{n}] = P [X_{1} \leq x_{1}] . . . . P [X_{n} \leq x_{n}] .$

6 / 38

Simple time series models

1. iid noise

no trend or seasonal component
observations are independent and identically distributed (iid) random variables with zero mean.
Notation: ${X_{t}} \sim I I D (0, σ^{2})$
plays an important role as a building block for more complicated time series.

Joint distribution function of iid noise

$P [X_{1} \leq x_{1}, X_{2} \leq x_{2}, . . ., X_{n} \leq x_{n}] = P [X_{1} \leq x_{1}] . . . . P [X_{n} \leq x_{n}] .$ Let $F_{X} (.)$ be the cumulative distribution function of each of the identically distributed random variables $X_{1}, X_{2}, . . .$ Then, $P [X_{1} \leq x_{1}, X_{2} \leq x_{2}, . . ., X_{n} \leq x_{n}] = F_{X} (x_{1}) . . . F_{X} (x_{n})$

6 / 38

Simple time series models

1. iid noise

no trend or seasonal component
observations are independent and identically distributed (iid) random variables with zero mean.
Notation: ${X_{t}} \sim I I D (0, σ^{2})$
plays an important role as a building block for more complicated time series.

Joint distribution function of iid noise

6 / 38

iid noise (cont.)

Examples of iid noise

Sequence of iid random variables ${X_{t}, t = 1, 2, . . .}$ with $P (X_{t} = 1) = \frac{1}{2}$ and $P (X_{t} = 0) = \frac{1}{2} .$

rnorm(15)

 [1]  2.61665472 -1.47748881 -0.75695121 -1.70520956 -1.02075354  0.81739417
 [7]  0.01909737 -1.29025062  0.84205925  0.27636792 -1.37133390 -0.89830051
[13] -0.62070173  0.15142641  0.40849453

7 / 38

iid noise (cont.)

Examples of iid noise

Sequence of iid random variables ${X_{t}, t = 1, 2, . . .}$ with $P (X_{t} = 1) = \frac{1}{2}$ and $P (X_{t} = 0) = \frac{1}{2} .$

rnorm(15)

 [1]  2.61665472 -1.47748881 -0.75695121 -1.70520956 -1.02075354  0.81739417
 [7]  0.01909737 -1.29025062  0.84205925  0.27636792 -1.37133390 -0.89830051
[13] -0.62070173  0.15142641  0.40849453

Question

Let ${X_{t}}$ is a iid noise with $E (X^{2}) = σ^{2} < \infty$ . Show that ${X_{t}}$ is a stationary process.

7 / 38

Simple time series models

2. White noise

If ${X_{t}}$ is a sequence of uncorrelated random variables, each with zero mean and variance $σ^{2}$ , then such a sequence is referred to as white noise.

Note: Every $I I D (0, σ^{2})$ sequence is $W N (0, σ^{2})$ but not conversely.

8 / 38

Simple time series models

3. Random walk

A random walk process is obtained by cumulatively summing iid random variables. If ${S_{t}, t = 0, 1, 2, . . .}$ is a random walk process, then $S_{0} = 0$

$S_{1} = 0 + X_{1}$

$S_{2} = 0 + X_{1} + X_{2}$

$. . .$

$S_{t} = X_{1} + X_{2} + . . . + X_{t} .$

9 / 38

Simple time series models

3. Random walk

A random walk process is obtained by cumulatively summing iid random variables. If ${S_{t}, t = 0, 1, 2, . . .}$ is a random walk process, then $S_{0} = 0$

$S_{1} = 0 + X_{1}$

$S_{2} = 0 + X_{1} + X_{2}$

$. . .$

$S_{t} = X_{1} + X_{2} + . . . + X_{t} .$

Question

Is ${S_{t}, t = 0, 1, 2, . . .}$ a weak stationary process?

9 / 38

Identifying non-stationarity in the mean

Using time series plot
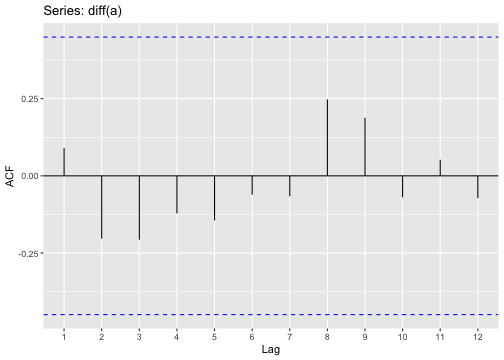
ACF plot
- ACF of stationary time series will drop to relatively quickly.
- The ACF of non-stationary series decreases slowly.
- For non-stationary series, the ACF at lag 1 is often large and positive.

10 / 38

Elimination of Trend and Seasonality by Differencing

Differencing helps to stabilize the mean.

Backshift notation:

$B X_{t} = X_{t - 1}$

Ordinary differencing

The first-order differencing can be defined as

$\nabla X_{t} = X_{t} - X_{t - 1} = X_{t} - B X_{t} = (1 - B) X_{t}$ where $\nabla = 1 - B$ .

The second-order differencing

$\nabla^{2} X_{t} = \nabla (\nabla X_{t}) = \nabla (X_{t} - X_{t - 1}) = \nabla X_{t} - \nabla X_{t - 1} = (X_{t} - X_{t - 1}) - (X_{t - 1} - X_{t - 2})$

In practice, we seldom need to go beyond second order differencing.

11 / 38

Seasonal differencing

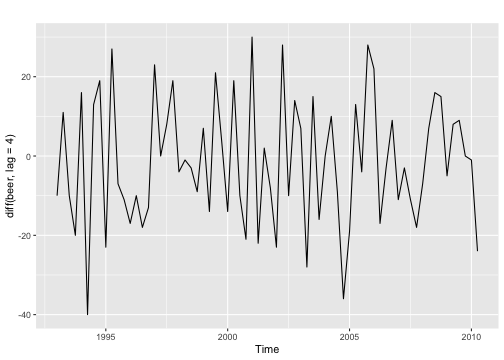
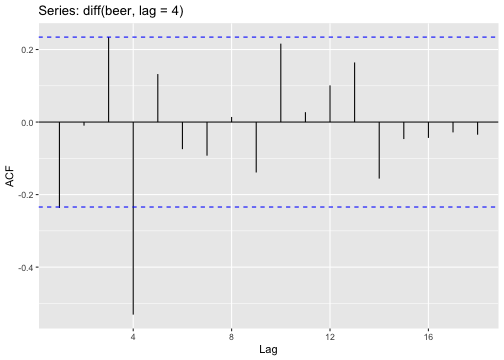
differencing between an observation and the corresponding observation from the previous year.

$\nabla_{m} X_{t} = X_{t} - X_{t - m} = (1 - B^{m}) X_{t}$ where $m$ is the number of seasons. For monthly, $m = 12$ , for quarterly $m = 4$ .

For monthly series

$\nabla_{12} X_{t} = X_{t} - X_{t - 12}$

Twice-differenced series

$\nabla_{12}^{2} X_{t} = \nabla_{12} X_{t} - \nabla_{12} X_{t - 1} = (X_{t} - X_{t - 12}) - (X_{t - 1} - X_{t - 13})$

If seasonality is strong, the seasonal differencing should be done first.

12 / 38

Original series

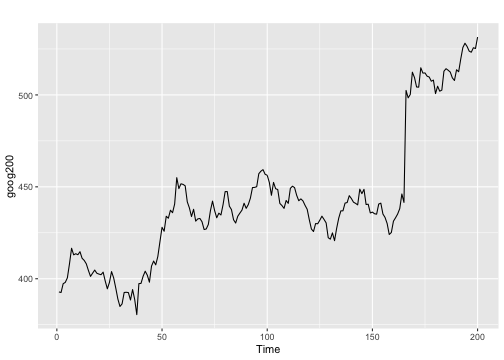
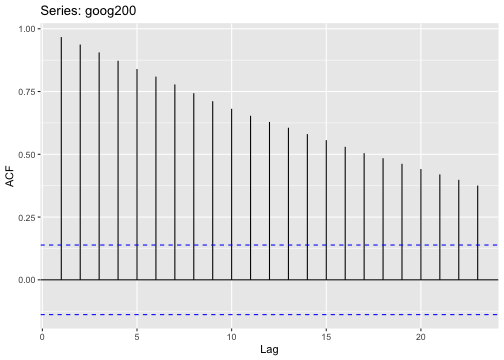
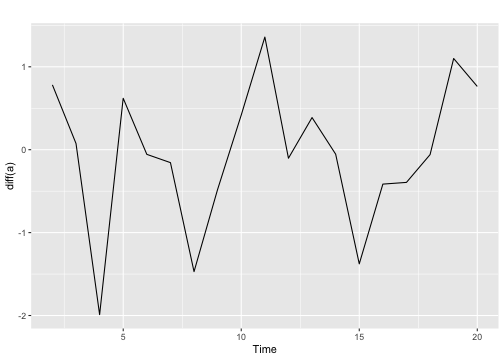
Differenced series

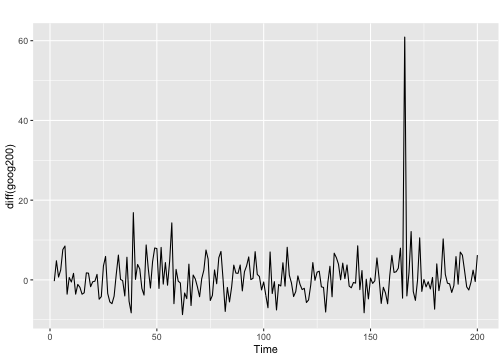
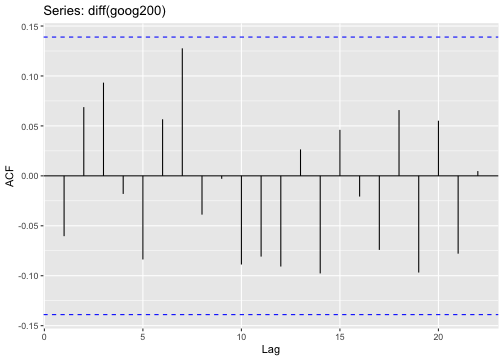
For a stationary time series, the ACF will drop to zero relatively quickly, while the ACF of non-stationary data decreases slowly.

13 / 38

Original series

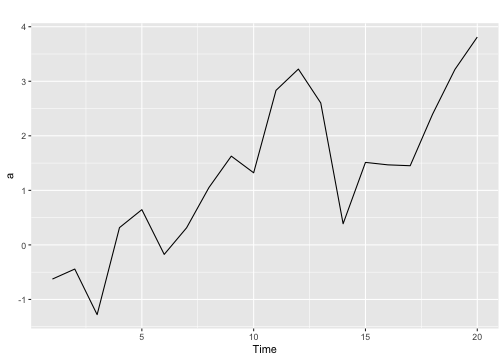
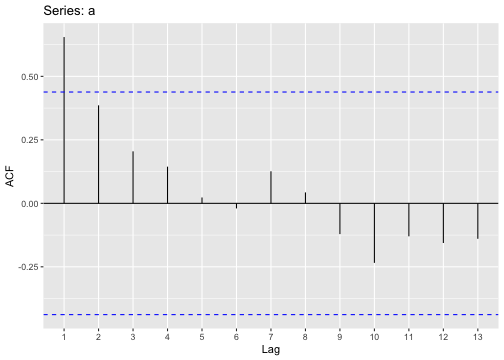
Differenced series

14 / 38

Original series

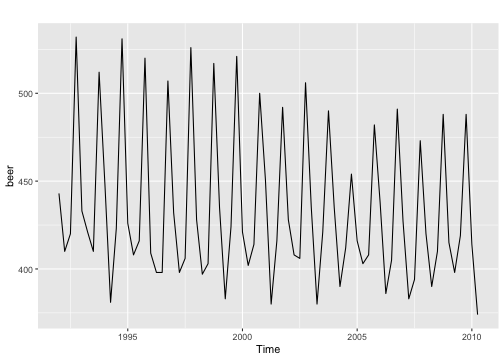
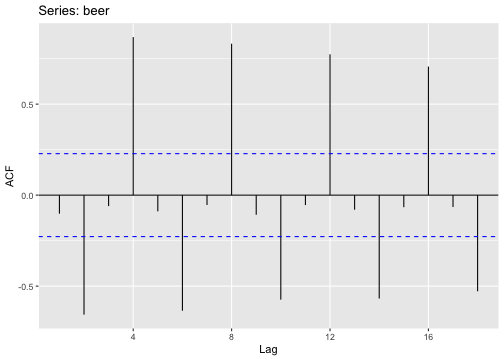
Seasonal Differencing

15 / 38

Linear filter model

A linear filter is an operation $L$ which transform the white noise process into another time series ${X_{t}}$ .

White noise $ϵ_{t}$ $\to$ Linear Filter $ψ (B)$ $\to$ Output $X_{t}$

16 / 38

Autoregressive models

current value = linear combination of past values + current error

An autoregressive model of order $p$ , $A R (P)$ model can be written as

$x_{t} = c + ϕ_{1} x_{t - 1} + ϕ_{2} x_{t - 2} + . . . + ϕ_{p} x_{t - p} + ϵ_{t},$ where $ϵ_{t}$ is white noise.

Similar to multiple linear regression model but with lagged values of $x_{t}$ as predictors.

17 / 38

Autoregressive models

current value = linear combination of past values + current error

An autoregressive model of order $p$ , $A R (P)$ model can be written as

$x_{t} = c + ϕ_{1} x_{t - 1} + ϕ_{2} x_{t - 2} + . . . + ϕ_{p} x_{t - p} + ϵ_{t},$ where $ϵ_{t}$ is white noise.

Similar to multiple linear regression model but with lagged values of $x_{t}$ as predictors.

Question

Show that $A R (P)$ is a linear filter with transfer function $ϕ^{- 1} (B)$ , where $ϕ (B) = 1 - ϕ_{1} B - ϕ_{2} B^{2} - . . . - ϕ_{p} B^{p} .$

17 / 38

Autoregressive models

current value = linear combination of past values + current error

An autoregressive model of order $p$ , $A R (P)$ model can be written as

$x_{t} = c + ϕ_{1} x_{t - 1} + ϕ_{2} x_{t - 2} + . . . + ϕ_{p} x_{t - p} + ϵ_{t},$ where $ϵ_{t}$ is white noise.

Similar to multiple linear regression model but with lagged values of $x_{t}$ as predictors.

Question

Show that $A R (P)$ is a linear filter with transfer function $ϕ^{- 1} (B)$ , where $ϕ (B) = 1 - ϕ_{1} B - ϕ_{2} B^{2} - . . . - ϕ_{p} B^{p} .$

Stationary condition for AR(P)

The roots of $ϕ (B) = 0$ (characteristic equation) must lie outside the unit circle.

17 / 38

Stationarity Conditions for AR(1)

Let's consider $A R (1)$ process,

$x_{t} = ϕ_{1} x_{t - 1} + ϵ_{t} .$

Then,

$(1 - ϕ_{1} B) x_{t} = ϵ_{t} .$

This may be written as, $x_{t} = (1 - ϕ_{1} B)^{- 1} ϵ_{t} = \sum_{j = 0}^{\infty} ϕ_{1}^{j} ϵ_{t - j} .$ Hence,

$ψ (B) = (1 - ϕ_{1} B)^{- 1} = \sum_{j = 0}^{\infty} ϕ_{1}^{j} B^{j}$

If $| ϕ_{1} | < 1,$ the $A R (1)$ process is stationary.

This is equivalent to saying the roots of $1 - ϕ_{1} B = 0$ must lie outside the unit circle.

18 / 38

Geometric series

$a + a r + a r^{2} + a r^{3} + . . . = \frac{a}{1 - r}$

for $| r | < 1.$

19 / 38

AR(1) process

$x_{t} = c + ϕ_{1} x_{t - 1} + ϵ_{t},$

when $ϕ_{1} = 0$ - equivalent to white noise process
when $ϕ_{1} = 0$ and $c = 0$ - random walk
when $ϕ_{1} = 1$ and $c \neq 0$ - random walk with drift
when $ϕ_{1} < 0$ - oscillates around the mean

20 / 38

Find the mean, variance and the autocorrelation function of a AR(1) process.

Help:

$C o v (X + Y, X + Y) = V a r (X + Y) = V a r (X) + V a r (Y) + 2 C o v (X, Y)$ $C o v (X, Y) = E [(X - μ_{X}) (Y - μ_{Y})]$

21 / 38

Question: Properties of AR(2) process

Find the Mean, Variance and Autocorrelation function.

22 / 38

Yule-Walker Equations

Autoregressive parameters in terms of the autocorrelations.

23 / 38

Autocorrelation function of a AR(P) process

The autocorrelation function of AR(P) process

$ρ_{k} = ϕ_{1} ρ_{k - 1} + ϕ_{2} ρ_{k - 2} + . . . + ϕ_{p} ρ_{k - p}$ for $k > 0$ .

This can be written as

$ϕ (B) ρ_{k} = 0,$ where $ϕ (B) = 1 - ϕ_{1} B - . . . - ϕ_{p} B^{p} .$

For $A R (1)$ process

$ρ_{k} = ϕ_{1} ρ_{k - 1},$ for $k > 0$ . Since $ρ_{0} = 1,$ for $k \geq 1$ , we get

$ρ_{k} = ϕ_{1}^{k}$

When $ϕ_{1} > 0$ , autocorrelation function decays exponentially to zero.
When $ϕ_{1} < 0$ , autocorrelation function decays exponentially to zero and oscillates in sign.

24 / 38

Partial Autocorrelation Function

Conditional autocorrelation between $X_{t}$ and $X_{t - k}$ given that $X_{t + 1}, X_{t + 2}, . . ., X_{t + k - 1}$ .

$C o r (X_{t}, X_{t + k} | X_{t + 1}, X_{t + 2}, . . ., X_{t + k - 1})$

The partial autocorrelation function $ϕ_{k k}$ of $A R (P)$ will be non-zero for $k$ less than or equal to $p$ and zero for $k$ greater than $p$ .

Calculations: in-class

25 / 38

Moving average models

Current value = linear combination of past forecast errors + current error

An $M A (q)$ process can be written as

$x_{t} = c + ϵ_{t} + θ_{1} ϵ_{t - 1} + θ_{2} ϵ_{t - 2} + . . . + θ_{p} ϵ_{t - q}$ where $ϵ_{t}$ is white noise.

The current value $x_{t}$ can be thought of as a weighted moving average of the past few forecast errors.
$M A (q)$ is always stationary.

26 / 38

Moving average models

Current value = linear combination of past forecast errors + current error

An $M A (q)$ process can be written as

$x_{t} = c + ϵ_{t} + θ_{1} ϵ_{t - 1} + θ_{2} ϵ_{t - 2} + . . . + θ_{p} ϵ_{t - q}$ where $ϵ_{t}$ is white noise.

The current value $x_{t}$ can be thought of as a weighted moving average of the past few forecast errors.
$M A (q)$ is always stationary.

Any $A R (p)$ model can be written as an $M A (\infty)$ model using repeated substitution.

26 / 38

Invertibility condition of an MA model

$x_{t} = c + ϵ_{t} + θ_{1} ϵ_{t - 1} + θ_{2} ϵ_{t - 2} + . . . + θ_{p} ϵ_{t - q}$ Using back shift operator, $x_{t} = c + ϵ_{t} + θ_{1} B ϵ_{t} + θ_{2} B^{2} ϵ_{t} + . . . + θ_{p} B^{q} ϵ_{t}$

Hence,

$x_{t} = θ_{q} (B) ϵ_{t} + c .$

The $θ_{q}$ is defined as an MA operator.

Any $M A (q)$ process can be written as an $A R (\infty)$ process if we impose some constraints on the MA parameters. Then it is called invertible.

MA model is called invertible if the roots of $θ_{q} (B) = 0$ lie outside the unit circle.

27 / 38

MA(1) process

Obtain the invertibility condition of $M A (1)$ process.
Calculate mean, variance, ACF and PACF of $M A (1)$ process.

28 / 38

MA(2) process

Calculate mean, variance, ACF and PACF of $M A (2)$ process.

29 / 38

ACF and PACF of AR(p) v MA(q) process

AR(p)

ACF: decays exponentially to zero.

PACF: PACF of $A R (p)$ process is zero, beyond the order $p$ of the process/ cut-off after lag $p$ .

MA(q)

ACF: ACF of $M A (q)$ process is zero, beyond the order $q$ of the process/ cut-off after lag $q$ .

PACF: decays exponentially to zero.

30 / 38

ARMA process

current value = linear combination of past values + linear combination of past error + current error

The $A R M A (p, q)$ can be written as

$X_{t} = c + ϕ_{1} x_{t - 1} + ϕ_{2} x_{t - 2} + . . . + ϕ_{p} x_{t - p} + θ_{1} ϵ_{t - 1} + θ_{2} ϵ_{t - 2} + . . . + θ_{q} ϵ_{t - q} + ϵ_{t},$ where ${ϵ_{t}}$ is a white noise process.

Using the back shift operator

$ϕ (B) x_{t} = θ (B) ϵ_{t},$ where $ϕ (.)$ and $θ (.)$ are the $p$ th and $q$ th degree polynomials,

$ϕ (B) = 1 - ϕ_{1} ϵ - . . . - ϕ_{p} ϵ^{p},$ and $θ (B) = 1 + θ_{1} ϵ + . . . + θ_{q} ϵ^{q} .$

31 / 38

ARMA(p, q) process

Stationary condition

Roots of $ϕ (B) = 0$ lie outside the unit circle.

Invertible condition

Roots of $θ (B) = 0$ lie outside the unit circle.

32 / 38

Question:

Determine which of the following processes are invertible and stationary.

$x_{t} = 0.6 x_{t - 1} + ϵ_{t}$
$x_{t} = ϵ_{t} - 1.3 ϵ_{t - 1} + 0.4 ϵ_{t - 2}$
$x_{t} = 0.6 x_{t - 1} - 1.3 ϵ_{t - 1} + 0.4 ϵ_{t - 2} + ϵ_{t}$
$x_{t} = x_{t - 1} - 1.3 ϵ_{t - 1} + 0.3 ϵ_{t - 2} + x_{t}$

33 / 38

ARMA(1, 1) model

Calculate the mean,variance and ACF of ARMA(1, 1) process.

34 / 38

Non-seasonal ARIMA models

Autoregressive Integrated Moving Average Model

$x_{t}^{'} = c + ϕ_{1} x_{t - 1}^{'} + . . . + ϕ_{p} x_{t - p}^{'} + θ_{1} ϵ_{t - 1} + . . . + θ_{q} ϵ_{t - q} + ϵ_{t},$ where $x_{t}^{'}$ is the difference series.

Using the back shift notation

$(1 - ϕ_{1} B - . . . - ϕ_{p} B^{p}) (1 - B)^{d} x_{t} = c + (1 + θ_{1} B + . . . + θ_{q} B^{q}) ϵ_{t}$

We call this an $A R I M A (p, d, q)$ model.
- p - order of the autoregressive part
- d - degree of first differencing involved
- q - order of the moving average part

35 / 38

Seasonal ARIMA model

Seasonal differencing

For monthly series

$(1 - B^{12}) x_{t} = x_{t} - x_{t - 12}$

For quarterly series

$(1 - B^{4}) x_{t} = x_{t} - x_{t - 4}$

Non-seasonal differencing

$(1 - B) x_{t} = x_{t} - x_{t - 1}$

Multiply terms together

$(1 - B) (1 - B^{m}) x_{t} = (1 - B - B^{m} + B^{m + 1}) x_{t} = x_{t} - x_{t - 1} - x_{t - m} + x_{t - m - 1} .$

36 / 38

Seasonal ARIMA models

$A R M A (p, d, q) (P, D, Q)_{m}$

$(p, d, q)$ - non-seasonal part of the model
$(P, D, Q)$ - seasonal part of the model
$m$ - number of observations per year

$A R I M A (1, 1, 1) (1, 1, 1)_{4}$

$(1 - ϕ_{1} B) (1 - Φ_{1} B^{4}) (1 - B) (1 - B^{4}) x_{t} = (1 + θ_{1} B) (1 + Θ_{1} B^{4}) ϵ_{t}$

$(1 - ϕ_{1} B)$ - Non-seasonal $A R (1)$

$(1 - Φ_{1} B^{4})$ - Seasonal $A R (1)$

$(1 - B)$ - Non-seasonal difference

$(1 - B^{4})$ - Deasonal difference

$(1 + θ_{1} B)$ - Non-seasonal $M A (1)$

$(1 + Θ B^{4})$ - Seasonal $M A (1)$

37 / 38

Question

Write down the model for

$A R I M A (0, 0, 1) (0, 0, 1)_{12}$ $A R I M A (1, 0, 0) (1, 0, 0)_{12}$

38 / 38

↑, ←, Pg Up, k	Go to previous slide
↓, →, Pg Dn, Space, j	Go to next slide
Home	Go to first slide
End	Go to last slide
Number + Return	Go to specific slide
b / m / f	Toggle blackout / mirrored / fullscreen mode
c	Clone slideshow
p	Toggle presenter mode
s	Start & Stop the presentation timer
t	Reset the presentation timer
?, h	Toggle this help